Lógica fuzzy
A lógica fuzzy é uma teoria matemática que lida com conceitos imprecisos ou vagos, permitindo que a linguagem natural seja utilizada para representar e manipular informações imprecisas.
Ela é uma extensão da lógica clássica binária, que utiliza apenas valores verdadeiro ou falso, permitindo a utilização de valores parcialmente verdadeiros em níveis de pertinência ou graus de verdade.
A lógica fuzzy é amplamente utilizada em sistemas de controle, inteligência artificial, robótica, análise de dados e tomada de decisões.
Lógica convencional: sim/não, verdadeiro/falso
Lógica Fuzzy:
- Muito similar ao pensamento humano;
- Tenta modelar o nosso senso de palavras, tomada de decisão ou senso comum
- Trabalha com uma grande variedade de informações vagas e incertas, as quais podem ser traduzidas por expressões do tipo: a maioria, mais ou menos, talvez, etc.
Conjuntos com limites imprecisos
A = Conjunto de pessoas altas
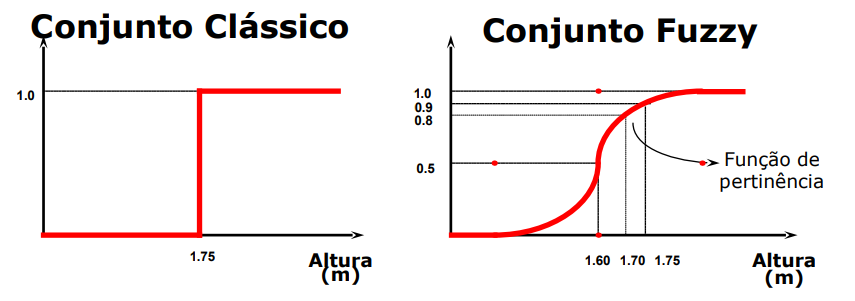
Suponha que desejássemos representar de forma fuzzy a altura de Alice (1,65 m), Bob (1,75 m), Carlos(2,0m) e Denise(1,45 m). Nossas proposições serão da forma "X é alto", e serão:
- A = Alice é alta, μ(A)=0,55
- B = Bob é alto, μ(B)=0,75
- C = Carlos é alto, μ(C) = 1,0
- D = Denise é alta, μ(D) = 0,0
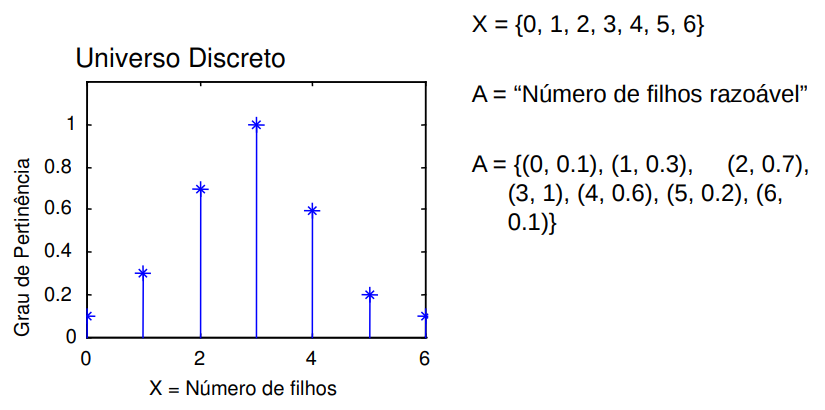
Um conjunto fuzzy A definido no universo X é caracterizado por uma função de pertinência uA, a qual mapeia os elementos de X para o intervalo [0,1]
Um conjunto fuzzy é totalmente caracterizado por sua função de pertinência
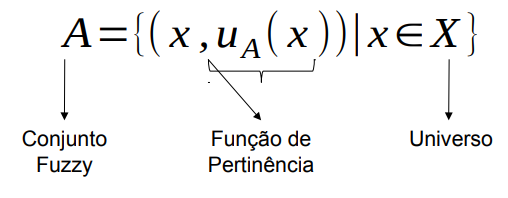
Função de Pertinencia para dados continuos
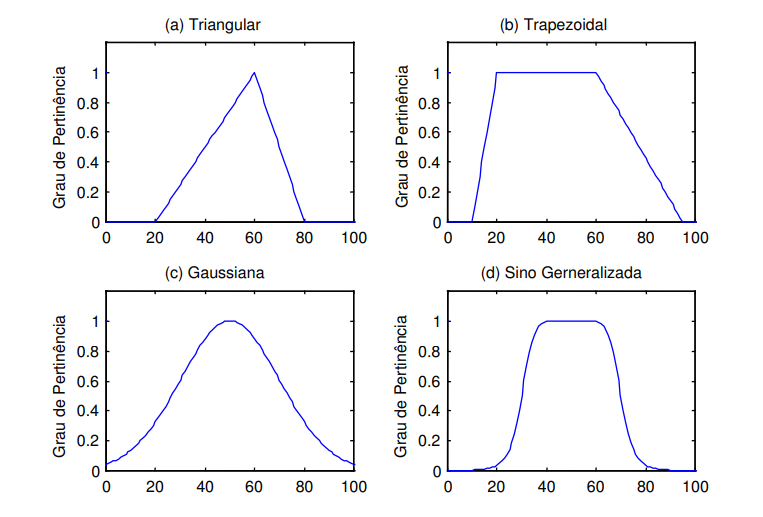
Função de pertinencia : Universo discreto
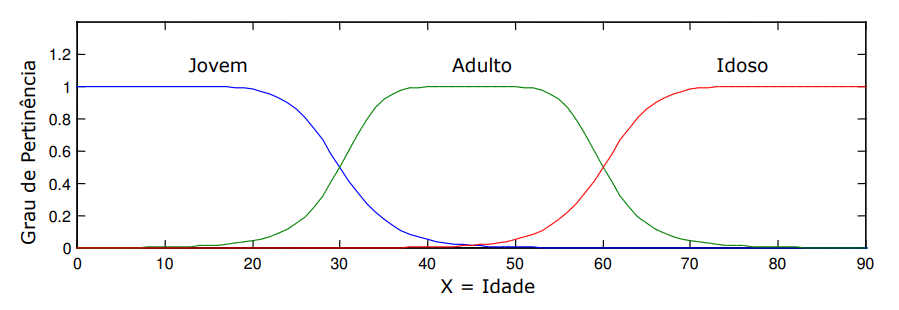
É uma partição do universo de discurso X representando “idade”, formada pelos conjuntos fuzzy “jovem”, “adulto” e “idoso”
Sistems de controle fuzzy
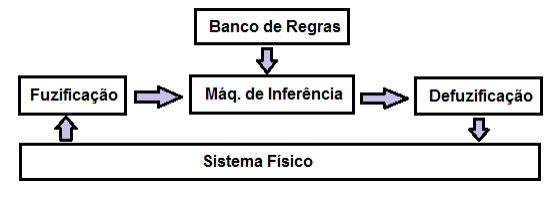
Componentes de um sistema de controle fuzzy
- Definição das variáveis fuzzy de entrada e de saída: forma e valores das variáveis
- Regras fuzzy
- Técnica de defuzzificação
Definição das variáveis
Etapa na qual as variáveis linguísticas são definidas de forma subjetiva, bem como as funções membro (funções de pertinência)
Engloba
- Análise do Problema
- Definição das Variáveis
- Definição das Funções de pertinência
- Criação das Regiões
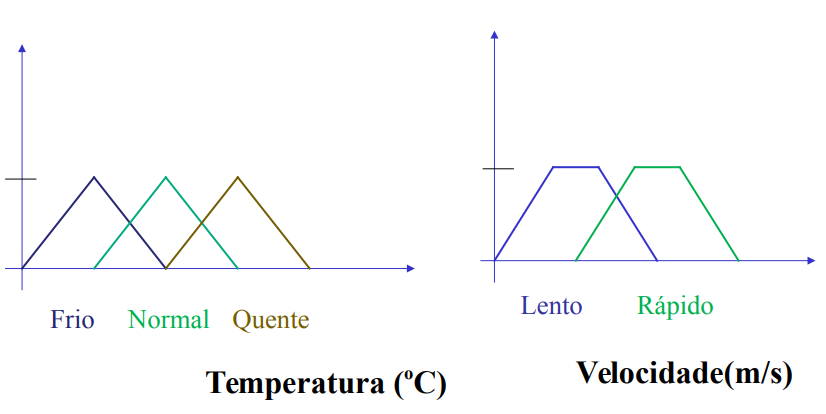
Na definição das funções de pertinência para cada variável, diversos tipos de espaço podem ser gerados:Triangular, Trapezoidal, Gaussiana, ...
Exemplos de variáveis fuzzy
Regras Fuzzy
SE condição ENTÃO conclusão , mas com variáveis linguísticas (fuzzy)
- Se a fruta é verde então o gosto é azedo
- Se a fruta é amarela então o gosto é pouco-doce
- Se a fruta é vermelha então o gosto é doce
Exemplo prático:
Vamos pesnar em um sistema fuzzy para tentar identificar a aderencia de uma pessoa ao curso de computação.
Na linguagem R para trabalharmos com fuzzy vamos utilizar o pacore: sets
Vamos definir nosso universo em valores que vão de 1 até 100
- sets_options("universe", seq(1,100, 1))
Variáveis linguisticas:
Na linguagem R teriamos
- fuzzy_partition(varnames = c( min = 5, men = 15, med = 50, maior=75, max=90), sd = 10)
Para o problema acima vamos inicializar as váriaveis conforme mostrado abaixo.
- Gosta_exatas = fuzzy_partition(varnames = c( gemin = 5, gemen = 15, gemed = 50, gemaior=75, gemax=90), sd = 10)
- Rel_interpess = fuzzy_partition(varnames = c( rimin = 30, rimen = 35, rimed = 55, rimaior=75,rimax=85), sd = 10)
- Escre_codigo = fuzzy_partition(varnames = c( ecmin = 10, ecmen = 25, ecmed = 50, ecmaior=75,ecmax=95), sd = 10)
- Pefil_lider = fuzzy_partition(varnames = c( plmin = 30, plmen = 50, plmed = 70, plmaior=90,plmax=95), sd=10)
- Gosta_Estudar = fuzzy_partition(varnames = c( gsmin = 20, gsmen = 40, gsmed = 60, gsmaior=80,gsmax=90), sd=10)
- Habilidade_comunicao = fuzzy_partition(varnames = c( hcmin = 40, hcmen = 50, hcmed = 60, hcmaior=70, hcmax=75), sd=10)
- Classificacao = fuzzy_partition(varnames = c( baixa = 10, media = 50, alta = 75, altissima=95), sd=10)
variaveis = set(v1,v2,v3,....)
Apos a inicialização das variáveis nós teriamos que montar as regras:
- fuzzy_rule( Gosta_exatas %is% gemax && Rel_interpess %is% rimin && Escre_codigo %is% ecmax && Pefil_lider %is% plmin && Gosta_Estudar %is% gsmax && Habilidade_comunicao %is% hcmin , Classificacao %is% altissima )
Quanto mais regras conseguirmos reproduzir, mas competo será nosso sistema
Para o nosso exemplo vamos construir 12 regras.
No R as regas serão agrupadas conforme abaixo
- regras <- set(regra1, regra2, regra3 ...)
A resposta é dado pelo comando:
- sistema <- fuzzy_system(variaveis, regras)
Construção das inferencias:
inferencia <- fuzzy_inference(sistema, list(v1 = 90 , v2 = 30, v3 = 95, v4 = 30, v5= 90, v6=40 ))
Impressão das respostas
Plotar
- sistema
- sistema$variables$Classificacao
- adicionar com o comando lines a inferencia: lines(inferencia, col = "red", lwd=4)
Pegar uma resposta: ,gset_defuzzify(inferencia, "centroid")
Parte visual: O objetivo é construir uma página conforme mostrado abaixo
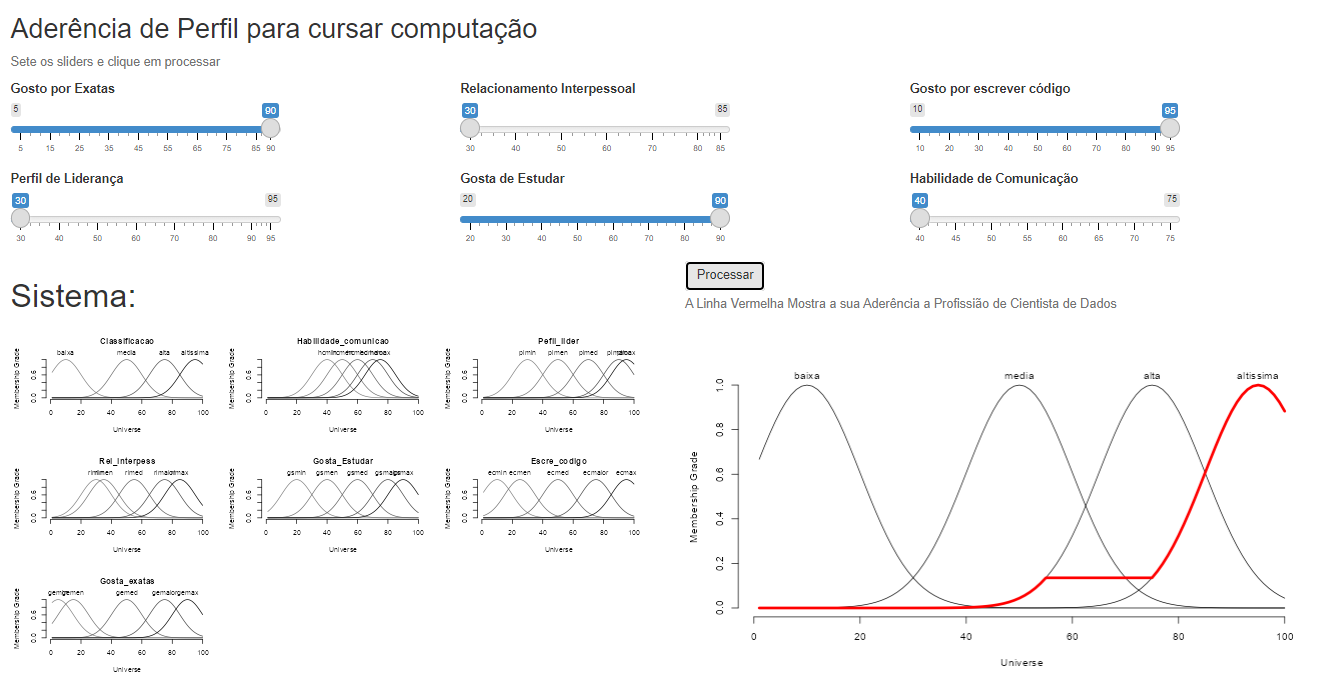
Novos componentes visuais
sliderInput("id", "Texto",min = Valor minimo, max = Valor máximo,step = passo,value = padrão)

Trabalho
Alternar Menu